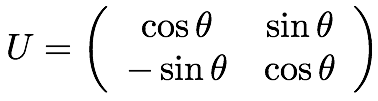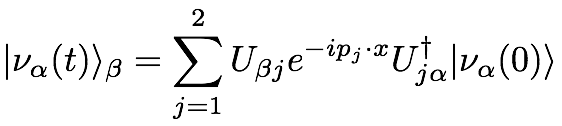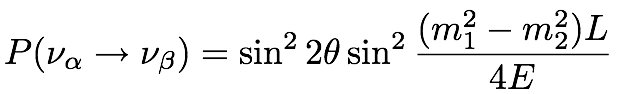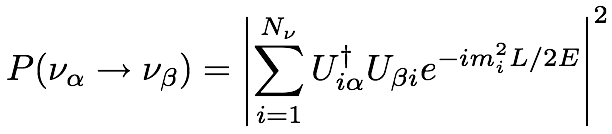Neutrino Oscillations
One of the interesting properties of neutrinos is that they can change from one type (or flavor) to another.
Neutrinos were originally conceived of as massless.
If all neutrinos had the same mass, then all states would be mass/energy eigenstates, and a neutrino created as one flavor (electron, muon, tau) would remain the same forever.
However, if neutrinos have mass, then the mass eigenstates need not be the same as the flavor eigenstates.
If that is true, then, for example, an electron neutrino is a superposition of the two mass eigenstates.
These eigenstates propagate in different ways, so that after some amount of time, the neutrino state evolves into a mix of electron, muon, and tau neutrinos.
To simplify things, assume for now that there are only two neutrinos.
Then there exists some unitary 2x2 matrix converting from the mass eigenstates (labeled with Latin indices) to the flavor eigenstates (labeled with Greek indices). That matrix can be generically written as:
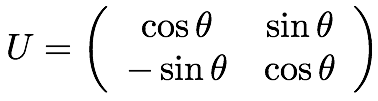
Note that this is not a generic unitary matrix. Some of the degrees of freedom of a generic matrix have no physical consequences and can be ignored.
While a rigorous treatment of the oscillation probability is fairly complicated, we can hand-wave a derivation (just don't think about the details too much since it doesn't really work).
If we assume a plane wave neutrino (actually a bad assumption) with energy E starting in flavor eigenstate α, then the state should evolve like:
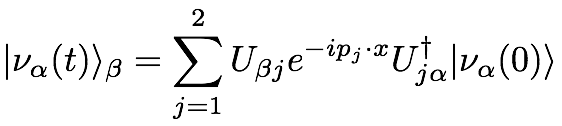
Expanding the momentum by factors of mi/E and assuming the neutrino travels at the speed of light, we see that the probability for the neutrino to oscillate into the other flavor β is:
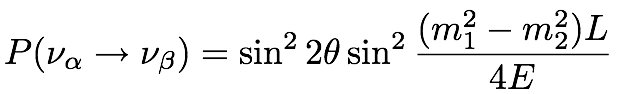
Expanding to three dimensions, the mixing matrix can have three mixing angles and a CP violating complex phase:

The three angles have been measured but to date, experiments have not yet been sensitive to the CP-violating phase δ.
This can be measured by finding differences in the oscillation probabilities for neutrinos and antineutrinos.
There is also a fourth matrix with two additional complex phases.
For massless neutrinos, for each type of neutrino there is a single left-handed neutrino state and a single right-handed antineutrino.
With massless neutrinos there are actually two possibilities: Left- and right-neutrinos and antineutrinos (a Dirac fermion) or left- and right-handed states which are antiparticles of one another (a Majorana fermion).
If a neutrino is it's own antiparticle (i.e. is a Majorana fermion) then there are these two additional phases.
Because Majorana fermions are their own antiparticles, they cannot carry an electric charge. Neutrinos are the only known neutral fermions and thus are the only known candidate for Majorana elementary particles.
Regardless, the oscillation probability for three neutrinos is:
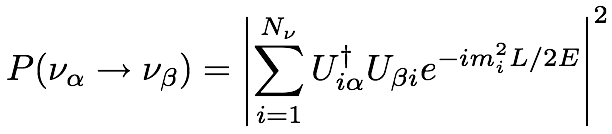
The probability depends on the differences between the squared masses — not the absolute mass scale — and the ratio of neutrino energy and distance between the two measurements.